Machine learning with H2O in R / Python
In this weblog, we’ll concentrate on about the best way to make use of H2O to assemble a few supervised machine learning fashions. H2O is a Java-based software program program for info modeling and regular computing, with the primary goal of it being a distributed, parallel, in memory processing engine. It have to be put in first (instructions) and by default an H2O event will run on localhost:54321. Additionally, one desires to place in R/python customers to to talk with the H2O event. Every new R / python session first should initialize a connection between the python client and the H2O cluster.
The points to be described in this weblog appeared in the exercise routines / initiatives in the Coursera course “Practical Machine Learning on H2O,” by H2O. The draw back statements / descriptions / steps are taken from the course itself. We shall use the concepts from the course, in order to:
- to assemble a few machine learning / deep learning fashions using completely totally different algorithms (corresponding to Gradient Boosting, Random Forest, Neural Net, Elastic Net GLM and so forth.),
- to analysis the standard bias-variance tradeoff (overfitting)
- for hyper-parameter tuning using Grid Search
- to utilize AutoML to routinely uncover a bunch of positive performing fashions
- to utilize Stacked Ensembles of fashions to boost effectivity.
Problem 1
In this draw back we’re going to create an artificial info set, then run random forest / GBM on it with H2O, to create two supervised fashions for classification, one which’s low-cost and one different one which reveals clear over-fitting. We will use R client (bundle) for H2O for this draw back.
- Let’s first create an info set to predict an employee’s job satisfaction in a company. Let’s say an employee’s job satisfaction is set by the subsequent components (there are a selection of various components in regular, nevertheless we’ll limit us to the subsequent few ones):
- work setting
- pay
- flexibility
- relationship with supervisor
- age
set.seed(321) # Let's say an employee's job satisfaction is set by the work setting, pay, flexibility, relationship with supervisor and age. N <- 1000 # number of samples d <- info.physique(id = 1:N) d$workEnvironment <- sample(1:5, N, alternate=TRUE) # on a scale of 1-5, 1 being unhealthy and 5 being good v <- spherical(rnorm(N, indicate=60000, sd=20000)) # 68% are 40-80k v <- pmax(v, 20000) v <- pmin(v, 100000) #desk(v) d$pay <- v d$flexibility <- sample(1:5, N, alternate=TRUE) # on a scale of 1-5, 1 being unhealthy and 5 being good d$managerRel <- sample(1:5, N, alternate=TRUE) # on a scale of 1-5, 1 being unhealthy and 5 being good d$age <- spherical(runif(N, min=20, max=60)) head(d) # id workEnvironment pay flexibility managerRel age #1 1 2 20000 2 2 21 #2 2 5 75817 1 2 31 #3 3 5 45649 5 3 25 #4 4 1 47157 1 5 55 #5 5 2 69729 2 4 33 #6 6 1 75101 2 2 39 v <- 125 * (d$pay/1000)^2 # e.g., job satisfaction score is proportional to sq. of pay (hypothetically) v <- v + 250 / log(d$age) # e.g., inversely proportional to log of age v <- v + 5 * d$flexibility v <- v + 200 * d$workEnvironment v <- v + 1000 * d$managerRel^3 v <- v + runif(N, 0, 5000) v <- 100 * (v - 0) / (max(v) - min(v)) # min-max normalization to ship the score in 0-100 d$jobSatScore <- spherical(v) # Round to nearest integer (proportion)2. Let’s start h2o, and import the data.
library(h2o) h2o.init() as.h2o(d, destination_frame = "jobsatisfaction") jobsat <- h2o.getFrame("jobsatisfaction") # |===========================================================================================================| 100% # id workEnvironment pay flexibility managerRel age jobSatScore #1 1 2 20000 2 2 21 5 #2 2 5 75817 1 2 31 55 #3 3 5 45649 5 3 25 22 #4 4 1 47157 1 5 55 30 #5 5 2 69729 2 4 33 51 #6 6 1 75101 2 2 39 54 3. Let’s minimize up the data. Here we plan to utilize cross-validation.
elements <- h2o.splitFrame( jobsat, ratios = 0.8, destination_frames=c("jobsat_train", "jobsat_test"), seed = 321) apply <- h2o.getFrame("jobsat_train") test <- h2o.getFrame("jobsat_test") norw(apply) # 794 norw(test) # 206 rows y <- "jobSatScore" x <- setdiff(names(apply), c("id", y)) 4. Let’s choose the gradient boosting model (gbm), and create a model. It’s a regression model given that output variable is dealt with to be regular.
# a budget model with 10-fold cross-validation m_res <- h2o.gbm(x, y, apply, model_id = "model10foldsreasonable", ntrees = 20, nfolds = 10, seed = 123) > h2o.effectivity(m_res, apply = TRUE) # RMSE 2.973807 #H2ORegressionMetrics: gbm #** Reported on teaching info. ** #MSE: 8.069509 #RMSE: 2.840688 #MAE: 2.266134 #RMSLE: 0.1357181 #Mean Residual Deviance : 8.069509 > h2o.effectivity(m_res, xval = TRUE) # RMSE 3.299601 #H2ORegressionMetrics: gbm #** Reported on cross-validation info. ** #** 10-fold cross-validation on teaching info (Metrics computed for combined holdout predictions) ** #MSE: 8.84353 #RMSE: 2.973807 #MAE: 2.320899 #RMSLE: 0.1384746 #Mean Residual Deviance : 8.84353 > h2o.effectivity(m_res, test) # RMSE 0.6476077 #H2ORegressionMetrics: gbm #MSE: 10.88737 #RMSE: 3.299601 #MAE: 2.524492 #RMSLE: 0.1409274 #Mean Residual Deviance : 10.88737 5. Let’s try some varied parameters, to assemble a singular model, and current how the outcomes differ.
# overfitting model with 10-fold cross-validation m_ovf <- h2o.gbm(x, y, apply, model_id = "model10foldsoverfitting", ntrees = 2000, max_depth = 20, nfolds = 10, seed = 123) > h2o.effectivity(m_ovf, apply = TRUE) # RMSE 0.004474786 #H2ORegressionMetrics: gbm #** Reported on teaching info. ** #MSE: 2.002371e-05 #RMSE: 0.004474786 #MAE: 0.0007455944 #RMSLE: 5.032019e-05 #Mean Residual Deviance : 2.002371e-05 > h2o.effectivity(m_ovf, xval = TRUE) # RMSE 0.6801615 #H2ORegressionMetrics: gbm #** Reported on cross-validation info. ** #** 10-fold cross-validation on teaching info (Metrics computed for combined holdout predictions) ** #MSE: 0.4626197 #RMSE: 0.6801615 #MAE: 0.4820542 #RMSLE: 0.02323415 #Mean Residual Deviance : 0.4626197 > h2o.effectivity(m_ovf, test) # RMSE 0.4969761 #H2ORegressionMetrics: gbm #MSE: 0.2469853 #RMSE: 0.4969761 #MAE: 0.3749822 #RMSLE: 0.01698435 #Mean Residual Deviance : 0.2469853Problem 2
Predict Chocolate Makers Location with Deep Learning Model with H2O
The info is accessible proper right here: http://coursera.h2o.ai/cacao.882.csv
This is a classification draw back. We must predict “Maker Location.” In totally different phrases, using the rating, and the other fields, how exactly we’re capable of set up whether or not it’s Belgian chocolate, French chocolate, and so forth. We shall use python client (library) for H2O for this draw back.
- Let’s start H2O, load the data set, and minimize up it. By the tip of this stage we should at all times have
three variables, pointing to three info frames on H2O: apply, authentic, test. However, in case you’re choosing to utilize
cross-validation, you will solely have two: apply and test.
import H2O import pandas as pd import numpy as np import matplotlib.pyplot as plt df = pd.read_csv('http://coursera.h2o.ai/cacao.882.csv') print(df.kind) # (1795, 9) df.head() | Maker | Origin | REF | Review Date | Cocoa Percent | Maker Location | Rating | Bean Type | Bean Origin | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | A. Morin | Agua Grande | 1876 | 2016 | 63% | France | 3.75 | Sao Tome | |
| 1 | A. Morin | Kpime | 1676 | 2015 | 70% | France | 2.75 | Togo | |
| 2 | A. Morin | Atsane | 1676 | 2015 | 70% | France | 3.00 | Togo | |
| 3 | A. Morin | Akata | 1680 | 2015 | 70% | France | 3.50 | Togo | |
| 4 | A. Morin | Quilla | 1704 | 2015 | 70% | France | 3.50 | Peru |
print(df['Maker Location'].distinctive()) # ['France' 'U.S.A.' 'Fiji' 'Ecuador' 'Mexico' 'Switzerland' 'Netherlands' # 'Spain' 'Peru' 'Canada' 'Italy' 'Brazil' 'U.K.' 'Australia' 'Wales' # 'Belgium' 'Germany' 'Russia' 'Puerto Rico' 'Venezuela' 'Colombia' 'Japan' # 'New Zealand' 'Costa Rica' 'South Korea' 'Amsterdam' 'Scotland' # 'Martinique' 'Sao Tome' 'Argentina' 'Guatemala' 'South Africa' 'Bolivia' # 'St. Lucia' 'Portugal' 'Singapore' 'Denmark' 'Vietnam' 'Grenada' 'Israel' # 'India' 'Czech Republic' 'Domincan Republic' 'Finland' 'Madagascar' # 'Philippines' 'Sweden' 'Poland' 'Austria' 'Honduras' 'Nicaragua' # 'Lithuania' 'Niacragua' 'Chile' 'Ghana' 'Iceland' 'Eucador' 'Hungary' # 'Suriname' 'Ireland'] print(len(df['Maker Location'].distinctive())) # 60 loc_table = df['Maker Location'].value_counts() print(loc_table) #U.S.A. 764 #France 156 #Canada 125 #U.Ok. 96 #Italy 63 #Ecuador 54 #Australia 49 #Belgium 40 #Switzerland 38 #Germany 35 #Austria 26 #Spain 25 #Colombia 23 #Hungary 22 #Venezuela 20 #Madagascar 17 #Japan 17 #New Zealand 17 #Brazil 17 #Peru 17 #Denmark 15 #Vietnam 11 #Scotland 10 #Guatemala 10 #Costa Rica 9 #Israel 9 #Argentina 9 #Poland 8 #Honduras 6 #Lithuania 6 #Sweden 5 #Nicaragua 5 #Domincan Republic 5 #South Korea 5 #Netherlands 4 #Amsterdam 4 #Puerto Rico 4 #Fiji 4 #Sao Tome 4 #Mexico 4 #Ireland 4 #Portugal 3 #Singapore 3 #Iceland 3 #South Africa 3 #Grenada 3 #Chile 2 #St. Lucia 2 #Bolivia 2 #Finland 2 #Martinique 1 #Eucador 1 #Wales 1 #Czech Republic 1 #Suriname 1 #Ghana 1 #India 1 #Niacragua 1 #Philippines 1 #Russia 1 #Name: Maker Location, dtype: int64 loc_table.hist() 
As will probably be seen from the above desk, a variety of the locations have too few info, which is ready to finish end result in poor accuracy of the model to be learnt on after splitting the dataset into apply, validation and test datasets. Let’s do away with the locations which have small number of (< 40) examples in the dataset, to make the outcomes further merely comprehendible, by reducing number of courses in the output variable.
## filter out the nations for which there's < 40 examples present in the dataset loc_gt_40_recs = loc_table[loc_table >= 40].index.tolist() df_sub = df[df['Maker Location'].isin(loc_gt_40_recs)] # now join with H2O h2o.init() # h2o.clusterStatus() | H2O cluster uptime: | 1 day 14 hours 48 minutes |
| H2O cluster mannequin: | 3.13.0.3978 |
| H2O cluster mannequin age: | 4 years and 9 days !!! |
| H2O cluster determine: | H2O_started_from_R_Sandipan.Dey_kpl973 |
| H2O cluster complete nodes: | 1 |
| H2O cluster free memory: | 2.530 Gb |
| H2O cluster complete cores: | 4 |
| H2O cluster allowed cores: | 4 |
| H2O cluster standing: | locked, healthful |
| H2O connection url: | http://localhost:54321 |
| H2O connection proxy: | None |
| H2O internal security: | False |
| H2O API Extensions: | Algos, AutoML, Core V3, Core V4 |
| Python mannequin: | 3.7.6 closing |
h2o_df = h2o.H2OFrame(df_sub.values, destination_frame = "cacao_882", column_names=[x.replace(' ', '_') for x in df.columns.tolist()]) #h2o_df.head() #h2o_df.summary() df_cacao_882 = h2o.get_frame('cacao_882') # df_cacao_882.as_data_frame() #df_cacao_882.head() df_cacao_882.describe() | Maker | Origin | REF | Review_Date | Cocoa_Percent | Maker_Location | Rating | Bean_Type | Bean_Origin | |
|---|---|---|---|---|---|---|---|---|---|
| form | enum | enum | int | int | enum | enum | precise | enum | enum |
| minutes | 5.0 | 2006.0 | 1.0 | ||||||
| indicate | 1025.8849294729039 | 2012.273942093541 | 3.1818856718633928 | ||||||
| maxs | 1952.0 | 2017.0 | 5.0 | ||||||
| sigma | 553.7812013716441 | 2.978615633185091 | 0.4911459825968248 | ||||||
| zeros | 0 | 0 | 0 | ||||||
| missing | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | A. Morin | Agua Grande | 1876.0 | 2016.0 | 63% | France | 3.75 | <0xA0> | Sao Tome |
| 1 | A. Morin | Kpime | 1676.0 | 2015.0 | 70% | France | 2.75 | <0xA0> | Togo |
| 2 | A. Morin | Atsane | 1676.0 | 2015.0 | 70% | France | 3.0 | <0xA0> | Togo |
| 3 | A. Morin | Akata | 1680.0 | 2015.0 | 70% | France | 3.5 | <0xA0> | Togo |
| 4 | A. Morin | Quilla | 1704.0 | 2015.0 | 70% | France | 3.5 | <0xA0> | Peru |
| 5 | A. Morin | Carenero | 1315.0 | 2014.0 | 70% | France | 2.75 | Criollo | Venezuela |
| 6 | A. Morin | Cuba | 1315.0 | 2014.0 | 70% | France | 3.5 | <0xA0> | Cuba |
| 7 | A. Morin | Sur del Lago | 1315.0 | 2014.0 | 70% | France | 3.5 | Criollo | Venezuela |
| 8 | A. Morin | Puerto Cabello | 1319.0 | 2014.0 | 70% | France | 3.75 | Criollo | Venezuela |
| 9 | A. Morin | Pablino | 1319.0 | 2014.0 | 70% | France | 4.0 | <0xA0> | Peru |
df_cacao_882['Maker_Location'].desk() #Maker_Location Count #Australia 49 #Belgium 40 #Canada 125 #Ecuador 54 #France 156 #Italy 63 #U.Ok. 96 #U.S.A. 764 apply, authentic, test = df_cacao_882.split_frame(ratios = [0.8, 0.1], destination_frames = ['train', 'valid', 'test'], seed = 321) print("%d/%d/%d" %(apply.nrows, authentic.nrows, test.nrows)) # 1082/138/127 2. Let’s set x to be the itemizing of columns we’ll use to teach on, to be the column we’ll examine. Here it’s going to be a multi-class classification draw back.
ignore_fields = ['Review_Date', 'Bean_Type', 'Maker_Location'] # Specify the response and predictor columns y = 'Maker_Location' # multinomial Classification x = [i for i in train.names if not i in ignore_fields]3. Let’s now create a baseline deep learning model. It is basically helpful to utilize all default settings (remembering to
specify each nfolds or validation_frame) for the baseline model.
from h2o.estimators.deeplearning import H2ODeepLearningEstimator model = H2ODeepLearningEstimator() %time model.apply(x = x, y = y, training_frame = apply, validation_frame = authentic) # deeplearning Model Build progress: |██████████████████████████████████████| 100% # Wall time: 6.44 s model.model_performance(apply).mean_per_class_error() # 0.05118279569892473 model.model_performance(authentic).mean_per_class_error() # 0.26888404593884047 perf_test = model.model_performance(test) print('Mean class error', perf_test.mean_per_class_error()) # Mean class error 0.2149184149184149 print('log loss', perf_test.logloss()) # log loss 0.48864148412056846 print('MSE', perf_test.mse()) # MSE 0.11940531127368789 print('RMSE', perf_test.rmse()) # RMSE 0.3455507361787671 perf_test.hit_ratio_table()Top-8 Hit Ratios:
| okay | hit_ratio |
| 1 | 0.8897638 |
| 2 | 0.9291338 |
| 3 | 0.9527559 |
| 4 | 0.9685039 |
| 5 | 0.9763779 |
| 6 | 0.9921259 |
| 7 | 0.9999999 |
| 8 | 0.9999999 |
perf_test.confusion_matrix().as_data_frame() | Australia | Belgium | Canada | Ecuador | France | Italy | U.Ok. | U.S.A. | Error | Rate | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.0 | 0.400000 | 2 / 5 |
| 1 | 0.0 | 2.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.333333 | 1 / 3 |
| 2 | 0.0 | 0.0 | 12.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.076923 | 1 / 13 |
| 3 | 0.0 | 0.0 | 0.0 | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0 / 3 |
| 4 | 0.0 | 0.0 | 0.0 | 0.0 | 8.0 | 2.0 | 0.0 | 1.0 | 0.272727 | 3 / 11 |
| 5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 10.0 | 0.0 | 0.0 | 0.000000 | 0 / 10 |
| 6 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 2.0 | 4.0 | 4.0 | 0.636364 | 7 / 11 |
| 7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 71.0 | 0.000000 | 0 / 71 |
| 8 | 3.0 | 2.0 | 12.0 | 4.0 | 8.0 | 15.0 | 4.0 | 79.0 | 0.110236 | 14 / 127 |
model.plot()
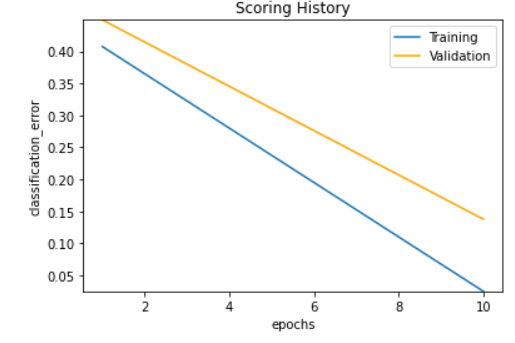
4. Now, let’s create a tuned model, that provides superior effectivity. However we should at all times use no more than 10 situations
the working time of your baseline model, so as soon as extra our script must be timing the model.
model_tuned = H2ODeepLearningEstimator(epochs=200, distribution="multinomial", activation="RectifierWithDropout", stopping_rounds=5, stopping_tolerance=0, stopping_metric="logloss", input_dropout_ratio=0.2, l1=1e-5, hidden=[200,200,200]) %time model_tuned.apply(x, y, training_frame = apply, validation_frame = authentic) #deeplearning Model Build progress: |██████████████████████████████████████| 100% #Wall time: 30.8 s model_tuned.model_performance(apply).mean_per_class_error() #0.0 model_tuned.model_performance(authentic).mean_per_class_error() #0.07696485401964853 perf_test = model_tuned.model_performance(test) print('Mean class error', perf_test.mean_per_class_error()) #Mean class error 0.05909090909090909 print('log loss', perf_test.logloss()) #log loss 0.14153784501504524 print('MSE', perf_test.mse()) #MSE 0.03497231075826773 print('RMSE', perf_test.rmse()) #RMSE 0.18700885208531637 perf_test.hit_ratio_table()Top-8 Hit Ratios:
| okay | hit_ratio |
| 1 | 0.9606299 |
| 2 | 0.984252 |
| 3 | 0.984252 |
| 4 | 0.992126 |
| 5 | 0.992126 |
| 6 | 0.992126 |
| 7 | 1.0 |
| 8 | 1.0 |
perf_test.confusion_matrix().as_data_frame()| Australia | Belgium | Canada | Ecuador | France | Italy | U.Ok. | U.S.A. | Error | Rate | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0 / 5 |
| 1 | 0.0 | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0 / 3 |
| 2 | 0.0 | 0.0 | 13.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0 / 13 |
| 3 | 0.0 | 0.0 | 0.0 | 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0 / 3 |
| 4 | 0.0 | 0.0 | 0.0 | 0.0 | 11.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0 / 11 |
| 5 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 8.0 | 0.0 | 1.0 | 0.200000 | 2 / 10 |
| 6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 8.0 | 3.0 | 0.272727 | 3 / 11 |
| 7 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 71.0 | 0.000000 | 0 / 71 |
| 8 | 5.0 | 3.0 | 13.0 | 3.0 | 12.0 | 8.0 | 8.0 | 75.0 | 0.039370 | 5 / 127 |
model_tuned.plot() 
As will probably be seen from the above plot, the early-stopping method stopped the model to overfit and the model achieves greater accruacy on the test dataset..
5. Let’s save every the fashions, to the native disk, using save_model(), to export the binary mannequin of the model. (Do not export a POJO.)
h2o.save_model(model, 'base_model') h2o.save_model(model_tuned, 'tuned_model')We might have to embody a seed in the model carry out above to get reproducible outcomes.
Problem 3
Predict Price of a house with Stacked Ensemble model with H2O
The info is accessible at http://coursera.h2o.ai/house_data.3487.csv. This is a regression draw back. We have to predict the “worth” of a house given completely totally different attribute values. We shall use python client for H2O as soon as extra for this draw back.
The info have to be minimize up into apply and test, using 0.9 for the ratio, and a seed of 123. That ought to offer 19,462 teaching rows and a few,151 test rows. The purpose is an RMSE underneath $123,000.
- Let’s start H2O, load the chosen dataset and observe the data manipulation steps. For occasion, we’re capable of minimize up date into 12 months and month columns. We can then optionally combine them proper right into a numeric date column. At the tip of this step we could have
apply,test,xandyvariables, and presumablyauthenticmoreover. The underneath reveals the code snippet to try this.
import h2o import pandas as pd import numpy as np import matplotlib.pyplot as plt import random from time import time h2o.init() url = "http://coursera.h2o.ai/house_data.3487.csv" house_df = h2o.import_file(url, destination_frame = "house_data") # Parse progress: |█████████████████████████████████████████████████████████| 100%Preporcessing
house_df['year'] = house_df['date'].substring(0,4).asnumeric() house_df['month'] = house_df['date'].substring(4,6).asnumeric() house_df['day'] = house_df['date'].substring(6,8).asnumeric() house_df = house_df.drop('date') house_df.head()| id | worth | bedrooms | bogs | sqft_living | sqft_lot | flooring | waterfront | view | scenario | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | prolonged | sqft_living15 | sqft_lot15 | 12 months | month | day |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.1293e+09 | 221900 | 3 | 1 | 1180 | 5650 | 1 | 0 | 0 | 3 | 7 | 1180 | 0 | 1955 | 0 | 98178 | 47.5112 | -122.257 | 1340 | 5650 | 2014 | 10 | 13 |
| 6.4141e+09 | 538000 | 3 | 2.25 | 2570 | 7242 | 2 | 0 | 0 | 3 | 7 | 2170 | 400 | 1951 | 1991 | 98125 | 47.721 | -122.319 | 1690 | 7639 | 2014 | 12 | 9 |
| 5.6315e+09 | 180000 | 2 | 1 | 770 | 10000 | 1 | 0 | 0 | 3 | 6 | 770 | 0 | 1933 | 0 | 98028 | 47.7379 | -122.233 | 2720 | 8062 | 2015 | 2 | 25 |
| 2.4872e+09 | 604000 | 4 | 3 | 1960 | 5000 | 1 | 0 | 0 | 5 | 7 | 1050 | 910 | 1965 | 0 | 98136 | 47.5208 | -122.393 | 1360 | 5000 | 2014 | 12 | 9 |
| 1.9544e+09 | 510000 | 3 | 2 | 1680 | 8080 | 1 | 0 | 0 | 3 | 8 | 1680 | 0 | 1987 | 0 | 98074 | 47.6168 | -122.045 | 1800 | 7503 | 2015 | 2 | 18 |
| 7.23755e+09 | 1.225e+06 | 4 | 4.5 | 5420 | 101930 | 1 | 0 | 0 | 3 | 11 | 3890 | 1530 | 2001 | 0 | 98053 | 47.6561 | -122.005 | 4760 | 101930 | 2014 | 5 | 12 |
| 1.3214e+09 | 257500 | 3 | 2.25 | 1715 | 6819 | 2 | 0 | 0 | 3 | 7 | 1715 | 0 | 1995 | 0 | 98003 | 47.3097 | -122.327 | 2238 | 6819 | 2014 | 6 | 27 |
| 2.008e+09 | 291850 | 3 | 1.5 | 1060 | 9711 | 1 | 0 | 0 | 3 | 7 | 1060 | 0 | 1963 | 0 | 98198 | 47.4095 | -122.315 | 1650 | 9711 | 2015 | 1 | 15 |
| 2.4146e+09 | 229500 | 3 | 1 | 1780 | 7470 | 1 | 0 | 0 | 3 | 7 | 1050 | 730 | 1960 | 0 | 98146 | 47.5123 | -122.337 | 1780 | 8113 | 2015 | 4 | 15 |
| 3.7935e+09 | 323000 | 3 | 2.5 | 1890 | 6560 | 2 | 0 | 0 | 3 | 7 | 1890 | 0 | 2003 | 0 | 98038 | 47.3684 | -122.031 | 2390 | 7570 | 2015 | 3 | 12 |
house_df.describe() | id | worth | bedrooms | bogs | sqft_living | sqft_lot | flooring | waterfront | view | scenario | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | prolonged | sqft_living15 | sqft_lot15 | 12 months | month | day | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| form | int | int | int | precise | int | int | precise | int | int | int | int | int | int | int | int | int | precise | precise | int | int | int | int | int |
| minutes | 1000102.0 | 75000.0 | 0.0 | 0.0 | 290.0 | 520.0 | 1.0 | 0.0 | 0.0 | 1.0 | 1.0 | 290.0 | 0.0 | 1900.0 | 0.0 | 98001.0 | 47.1559 | -122.519 | 399.0 | 651.0 | 2014.0 | 1.0 | 1.0 |
| indicate | 4580301520.864987 | 540088.1417665284 | 3.370841623097218 | 2.114757321982139 | 2079.899736269819 | 15106.96756581695 | 1.4943089807060526 | 0.007541757275713691 | 0.23430342849211097 | 3.4094295100171164 | 7.6568731781798105 | 1788.3906907879518 | 291.50904548188555 | 1971.0051357979064 | 84.4022579003377 | 98077.93980474674 | 47.56005251931665 | -122.21389640494158 | 1986.5524915560036 | 12768.45565169118 | 2014.3229537778102 | 6.574422801091883 | 15.688196918521294 |
| maxs | 9900000190.0 | 7700000.0 | 33.0 | 8.0 | 13540.0 | 1651359.0 | 3.5 | 1.0 | 4.0 | 5.0 | 13.0 | 9410.0 | 4820.0 | 2015.0 | 2015.0 | 98199.0 | 47.7776 | -121.315 | 6210.0 | 871200.0 | 2015.0 | 12.0 | 31.0 |
| sigma | 2876565571.3120522 | 367127.19648270035 | 0.930061831147451 | 0.7701631572177408 | 918.4408970468095 | 41420.51151513551 | 0.5399888951423489 | 0.08651719772788766 | 0.7663175692736117 | 0.6507430463662044 | 1.1754587569743344 | 828.0909776519175 | 442.57504267746685 | 29.373410802386235 | 401.67924001917555 | 53.50502625747248 | 0.13856371024192368 | 0.14082834238139297 | 685.3913042527788 | 27304.179631338524 | 0.4676160310451536 | 3.1153077787263648 | 8.635062534286034 |
| zeros | 0 | 0 | 13 | 10 | 0 | 0 | 0 | 21450 | 19489 | 0 | 0 | 0 | 13126 | 0 | 20699 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| missing | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 7129300520.0 | 221900.0 | 3.0 | 1.0 | 1180.0 | 5650.0 | 1.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1180.0 | 0.0 | 1955.0 | 0.0 | 98178.0 | 47.5112 | -122.257 | 1340.0 | 5650.0 | 2014.0 | 10.0 | 13.0 |
| 1 | 6414100192.0 | 538000.0 | 3.0 | 2.25 | 2570.0 | 7242.0 | 2.0 | 0.0 | 0.0 | 3.0 | 7.0 | 2170.0 | 400.0 | 1951.0 | 1991.0 | 98125.0 | 47.721000000000004 | -122.319 | 1690.0 | 7639.0 | 2014.0 | 12.0 | 9.0 |
| 2 | 5631500400.0 | 180000.0 | 2.0 | 1.0 | 770.0 | 10000.0 | 1.0 | 0.0 | 0.0 | 3.0 | 6.0 | 770.0 | 0.0 | 1933.0 | 0.0 | 98028.0 | 47.7379 | -122.233 | 2720.0 | 8062.0 | 2015.0 | 2.0 | 25.0 |
| 3 | 2487200875.0 | 604000.0 | 4.0 | 3.0 | 1960.0 | 5000.0 | 1.0 | 0.0 | 0.0 | 5.0 | 7.0 | 1050.0 | 910.0 | 1965.0 | 0.0 | 98136.0 | 47.5208 | -122.393 | 1360.0 | 5000.0 | 2014.0 | 12.0 | 9.0 |
| 4 | 1954400510.0 | 510000.0 | 3.0 | 2.0 | 1680.0 | 8080.0 | 1.0 | 0.0 | 0.0 | 3.0 | 8.0 | 1680.0 | 0.0 | 1987.0 | 0.0 | 98074.0 | 47.616800000000005 | -122.045 | 1800.0 | 7503.0 | 2015.0 | 2.0 | 18.0 |
| 5 | 7237550310.0 | 1225000.0 | 4.0 | 4.5 | 5420.0 | 101930.0 | 1.0 | 0.0 | 0.0 | 3.0 | 11.0 | 3890.0 | 1530.0 | 2001.0 | 0.0 | 98053.0 | 47.6561 | -122.005 | 4760.0 | 101930.0 | 2014.0 | 5.0 | 12.0 |
| 6 | 1321400060.0 | 257500.0 | 3.0 | 2.25 | 1715.0 | 6819.0 | 2.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1715.0 | 0.0 | 1995.0 | 0.0 | 98003.0 | 47.3097 | -122.327 | 2238.0 | 6819.0 | 2014.0 | 6.0 | 27.0 |
| 7 | 2008000270.0 | 291850.0 | 3.0 | 1.5 | 1060.0 | 9711.0 | 1.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1060.0 | 0.0 | 1963.0 | 0.0 | 98198.0 | 47.4095 | -122.315 | 1650.0 | 9711.0 | 2015.0 | 1.0 | 15.0 |
| 8 | 2414600126.0 | 229500.0 | 3.0 | 1.0 | 1780.0 | 7470.0 | 1.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1050.0 | 730.0 | 1960.0 | 0.0 | 98146.0 | 47.5123 | -122.337 | 1780.0 | 8113.0 | 2015.0 | 4.0 | 15.0 |
| 9 | 3793500160.0 | 323000.0 | 3.0 | 2.5 | 1890.0 | 6560.0 | 2.0 | 0.0 | 0.0 | 3.0 | 7.0 | 1890.0 | 0.0 | 2003.0 | 0.0 | 98038.0 | 47.3684 | -122.031 | 2390.0 | 7570.0 | 2015.0 | 3.0 | 12.0 |
plt.hist(house_df.as_data_frame()['price'].tolist(), bins=np.linspace(0,10**6,1000)) plt.current()
We shall use cross-validation and by no means a validation dataset.
apply, test = house_df.split_frame(ratios=[0.9], destination_frames = ['train', 'test'], seed=123) print("%d/%d" %(apply.nrows, test.nrows)) # 19462/2151 ignore_fields = ['id', 'price'] x = [i for i in train.names if not i in ignore_fields] y = 'worth' 2. Let’s now apply at least 4 completely totally different fashions on the preprocessed datseet, using at least three completely totally different supervised algorithms. Let’s save all the fashions.
from h2o.estimators.gbm import H2OGradientBoostingEstimator from h2o.estimators.random_forest import H2ORandomForestEstimator from h2o.estimators.glm import H2OGeneralizedLinearEstimator from h2o.estimators.deeplearning import H2ODeepLearningEstimator from h2o.estimators.stackedensemble import H2OStackedEnsembleEstimator nfolds = 5 # for cross-validation Let’s first match a GLM model. The best performing α hyperparameter value (for controlling L1 vs. L2 regularization) for GLM will most likely be found using GridSearch, as confirmed in the underneath code snippet.
g= h2o.grid.H2OGridSearch( H2OGeneralizedLinearEstimator(family="gaussian", nfolds=nfolds, fold_assignment="Modulo", keep_cross_validation_predictions=True, lambda_search=True), hyper_params={ "alpha":[x * 0.01 for x in range(0,100)], }, search_criteria={ "method":"RandomDiscrete", "max_models":8, "stopping_metric": "rmse", "max_runtime_secs":60 } ) g.apply(x, y, apply) g #glm Grid Build progress: |████████████████████████████████████████████████| 100% # alpha #0 [0.61] #1 [0.78] #2 [0.65] #3 [0.13] #4 [0.35000000000000003] #5 [0.05] #6 [0.32] #7 [0.55] # model_ids residual_deviance #0 Grid_GLM_train_model_python_1628864392402_41_model_3 2.626981989511134E15 #1 Grid_GLM_train_model_python_1628864392402_41_model_6 2.626981989511134E15 #2 Grid_GLM_train_model_python_1628864392402_41_model_5 2.626981989511134E15 #3 Grid_GLM_train_model_python_1628864392402_41_model_2 2.626981989511134E15 #4 Grid_GLM_train_model_python_1628864392402_41_model_4 2.626981989511134E15 #5 Grid_GLM_train_model_python_1628864392402_41_model_7 2.626981989511134E15 #6 Grid_GLM_train_model_python_1628864392402_41_model_0 2.626981989511134E15 #7 Grid_GLM_train_model_python_1628864392402_41_model_1 2.626981989511134E15 Model 1
model_GLM= H2OGeneralizedLinearEstimator( family='gaussian', #'gamma', model_id='glm_house', nfolds=nfolds, alpha=0.61, fold_assignment="Modulo", keep_cross_validation_predictions=True) %time model_GLM.apply(x, y, apply) #glm Model Build progress: |███████████████████████████████████████████████| 100% #Wall time: 259 ms model_GLM.cross_validation_metrics_summary().as_data_frame()| indicate | sd | cv_1_valid | cv_2_valid | cv_3_valid | cv_4_valid | cv_5_valid | ||
|---|---|---|---|---|---|---|---|---|
| 0 | mae | 230053.23 | 715.8795 | 229225.16 | 230969.69 | 228503.45 | 230529.47 | 231038.42 |
| 1 | mean_residual_deviance | 1.31780157E11 | 4.5671977E9 | 1.32968604E11 | 1.41431144E11 | 1.31364495E11 | 1.32024402E11 | 1.21112134E11 |
| 2 | mse | 1.31780157E11 | 4.5671977E9 | 1.32968604E11 | 1.41431144E11 | 1.31364495E11 | 1.32024402E11 | 1.21112134E11 |
| 3 | null_deviance | 5.25455325E14 | 1.80834544E13 | 5.3056184E14 | 5.636807E14 | 5.23549568E14 | 5.26203388E14 | 4.83281095E14 |
| 4 | r2 | 0.023522535 | 4.801036E-4 | 0.024299357 | 0.023168933 | 0.022531934 | 0.023340257 | 0.024272196 |
| 5 | residual_deviance | 5.12943247E14 | 1.7808912E13 | 5.17646773E14 | 5.5059142E14 | 5.11270625E14 | 5.13838982E14 | 4.71368433E14 |
| 6 | rmse | 362905.53 | 6314.0225 | 364648.6 | 376073.3 | 362442.4 | 363351.62 | 348011.7 |
| 7 | rmsle | 0.53911585 | 0.0047404445 | 0.54277176 | 0.5389013 | 0.5275475 | 0.53846484 | 0.54789394 |
model_GLM.model_performance(test) #ModelMetricsRegressionGLM: glm #** Reported on test info. ** #MSE: 128806123545.59714 #RMSE: 358895.7000934911 #MAE: 233890.6933813204 #RMSLE: 0.5456714021880726 #R^2: 0.03102347771355851 #Mean Residual Deviance: 128806123545.59714 #Null ranges of freedom: 2150 #Residual ranges of freedom: 2129 #Null deviance: 285935013037402.7 #Residual deviance: 277061971746579.44 #AIC: 61176.23965800522As will probably be seen from above, GLM could not receive the purpose of RMSE underneath $123k neither on cross-validation nor on test dataset.
The underneath fashions (GBM, DRF and DL) and the corresponding parameters have been found with AutoML leaderboard and
GridSearch, alongside with some handbook tuning.
from h2o.automl import H2OAutoML model_auto = H2OAutoML(max_runtime_secs=60, seed=123) model_auto.apply(x, y, apply) # AutoML progress: |████████████████████████████████████████████████████████| 100% # Parse progress: |█████████████████████████████████████████████████████████| 100% model_auto.leaderboard| model_id | mean_residual_deviance | rmse | mae | rmsle |
|---|---|---|---|---|
| GBM_grid_0_AutoML_20210814_005121_model_0 | 2.01725e+10 | 142030 | 77779.1 | 0.184269 |
| GBM_grid_0_AutoML_20210814_005121_model_1 | 2.6037e+10 | 161360 | 93068.1 | 0.218365 |
| DRF_0_AutoML_20210814_005121 | 3.27251e+10 | 180901 | 102782 | 0.243474 |
| XRT_0_AutoML_20210814_005121 | 3.53492e+10 | 188014 | 104259 | 0.246899 |
| GBM_grid_0_AutoML_20210813_201225_model_0 | 5.99803e+10 | 244909 | 153548 | 0.351959 |
| GBM_grid_0_AutoML_20210813_201225_model_2 | 6.09613e+10 | 246903 | 152570 | 0.349919 |
| GBM_grid_0_AutoML_20210813_201225_model_1 | 6.09941e+10 | 246970 | 153096 | 0.350852 |
| GBM_grid_0_AutoML_20210813_201225_model_3 | 6.22174e+10 | 249434 | 153105 | 0.350598 |
| DeepLearning_0_AutoML_20210813_201225 | 6.39672e+10 | 252917 | 163993 | 0.378761 |
| DRF_0_AutoML_20210813_201225 | 6.76936e+10 | 260180 | 158078 | 0.360337 |
model_auto.chief.model_performance(test) # model_auto.chief.make clear(test) #ModelMetricsRegression: gbm #** Reported on test info. ** #MSE: 17456681023.716145 #RMSE: 132123.73376390839 #MAE: 77000.00253466706 #RMSLE: 0.1899899418603569 #Mean Residual Deviance: 17456681023.716145 model = h2o.get_model(model_auto.leaderboard[4, 'model_id']) # get model by model_id print(model.params['model_id']['actual']['name']) print(model.model_performance(test).rmse()) [(k, v) for (k, v) in model.params.items() if v['default'] != v['actual'] and not okay in ['model_id', 'training_frame', 'validation_frame', 'nfolds', 'keep_cross_validation_predictions', 'seed', 'response_column', 'fold_assignment', 'ignored_columns']] # GBM_grid_0_AutoML_20210813_201225_model_0 # 235011.60404473927 # [('score_tree_interval', {'default': 0, 'actual': 5}), # ('ntrees', {'default': 50, 'actual': 60}), # ('max_depth', {'default': 5, 'actual': 6}), # ('min_rows', {'default': 10.0, 'actual': 1.0}), # ('stopping_tolerance', {'default': 0.001, 'actual': 0.008577452408351779}), # ('seed', {'default': -1, 'actual': 123}), # ('distribution', {'default': 'AUTO', 'actual': 'gaussian'}), # ('sample_rate', {'default': 1.0, 'actual': 0.8}), # ('col_sample_rate', {'default': 1.0, 'actual': 0.8}), # ('col_sample_rate_per_tree', {'default': 1.0, 'actual': 0.8})]Model 2
model_GBM = H2OGradientBoostingEstimator( model_id='gbm_house', nfolds=nfolds, ntrees=500, fold_assignment="Modulo", keep_cross_validation_predictions=True, seed=123) %time model_GBM.apply(x, y, apply) #gbm Model Build progress: |███████████████████████████████████████████████| 100% #Wall time: 54.9 s model_GBM.cross_validation_metrics_summary().as_data_frame()| indicate | sd | cv_1_valid | cv_2_valid | cv_3_valid | cv_4_valid | cv_5_valid | ||
|---|---|---|---|---|---|---|---|---|
| 0 | mae | 64136.496 | 912.2387 | 62751.688 | 66573.63 | 63946.31 | 63873.707 | 63537.137 |
| 1 | mean_residual_deviance | 1.38268457E10 | 1.43582912E9 | 1.24595825E10 | 1.75283814E10 | 1.2894718E10 | 1.43893801E10 | 1.18621655E10 |
| 2 | mse | 1.38268457E10 | 1.43582912E9 | 1.24595825E10 | 1.75283814E10 | 1.2894718E10 | 1.43893801E10 | 1.18621655E10 |
| 3 | r2 | 0.8979097 | 0.0075696795 | 0.90857375 | 0.87893564 | 0.9040519 | 0.89355356 | 0.90443367 |
| 4 | residual_deviance | 1.38268457E10 | 1.43582912E9 | 1.24595825E10 | 1.75283814E10 | 1.2894718E10 | 1.43893801E10 | 1.18621655E10 |
| 5 | rmse | 117288.305 | 5928.7188 | 111622.5 | 132394.8 | 113554.914 | 119955.74 | 108913.57 |
| 6 | rmsle | 0.16441989 | 0.0025737707 | 0.16231671 | 0.17041409 | 0.15941188 | 0.16528262 | 0.16467415 |
As will probably be seen from the above desk (row 5, column 1), the indicate RMSE for cross-validation is 117288.305, which is underneath $123k.
model_GBM.model_performance(test) #ModelMetricsRegression: gbm #** Reported on test info. ** #MSE: 14243079402.729088 #RMSE: 119344.37315068142 #MAE: 65050.344749203745 #RMSLE: 0.16421689257411975 #Mean Residual Deviance: 14243079402.729088As will probably be seen from above, GBM could receive the purpose of RMSE underneath $123k on test dataset.
Now, let’s try random forest model by discovering best parameters with Grid Search:
g= h2o.grid.H2OGridSearch( H2ORandomForestEstimator( nfolds=nfolds, fold_assignment="Modulo", keep_cross_validation_predictions=True, seed=123), hyper_params={ "ntrees": [20, 25, 30], "stopping_tolerance": [0.005, 0.006, 0.0075], "max_depth": [20, 50, 100], "min_rows": [5, 7, 10] }, search_criteria={ "method":"RandomDiscrete", "max_models":10, "stopping_metric": "rmse", "max_runtime_secs":60 } ) g.apply(x, y, apply) #drf Grid Build progress: |████████████████████████████████████████████████| 100% g # max_depth min_rows ntrees stopping_tolerance #0 100 5.0 20 0.006 #1 100 5.0 20 0.005 #2 100 5.0 20 0.005 #3 100 7.0 30 0.006 #4 50 10.0 25 0.006 #5 50 10.0 20 0.005 # model_ids residual_deviance #0 Grid_DRF_train_model_python_1628864392402_40_model_0 2.0205038467456142E10 #1 Grid_DRF_train_model_python_1628864392402_40_model_5 2.0205038467456142E10 #2 Grid_DRF_train_model_python_1628864392402_40_model_1 2.0205038467456142E10 #3 Grid_DRF_train_model_python_1628864392402_40_model_3 2.099520493338354E10 #4 Grid_DRF_train_model_python_1628864392402_40_model_2 2.260686283035833E10 #5 Grid_DRF_train_model_python_1628864392402_40_model_4 2.279037520277947E10 Model 3
model_RF = H2ORandomForestEstimator( model_id='rf_house', nfolds=nfolds, ntrees=20, fold_assignment="Modulo", keep_cross_validation_predictions=True, seed=123) %time model_RF.apply(x, y, apply) #drf Model Build progress: |███████████████████████████████████████████████| 100% #Wall time: 13.2 s model_RF.cross_validation_metrics_summary().as_data_frame()| indicate | sd | cv_1_valid | cv_2_valid | cv_3_valid | cv_4_valid | cv_5_valid | ||
|---|---|---|---|---|---|---|---|---|
| 0 | mae | 72734.0 | 1162.9153 | 73242.26 | 75062.21 | 73461.65 | 71646.195 | 70257.7 |
| 1 | mean_residual_deviance | 1.8545494E10 | 2.2018921E9 | 1.79095654E10 | 2.45911347E10 | 1.74433321E10 | 1.71117425E10 | 1.56716954E10 |
| 2 | mse | 1.8545494E10 | 2.2018921E9 | 1.79095654E10 | 2.45911347E10 | 1.74433321E10 | 1.71117425E10 | 1.56716954E10 |
| 3 | r2 | 0.8632202 | 0.011770816 | 0.8685827 | 0.8301549 | 0.8702062 | 0.8734147 | 0.8737426 |
| 4 | residual_deviance | 1.8545494E10 | 2.2018921E9 | 1.79095654E10 | 2.45911347E10 | 1.74433321E10 | 1.71117425E10 | 1.56716954E10 |
| 5 | rmse | 135742.78 | 7726.2373 | 133826.62 | 156815.61 | 132073.2 | 130811.86 | 125186.64 |
| 6 | rmsle | 0.18275535 | 0.0020155373 | 0.18441868 | 0.18689767 | 0.17945778 | 0.1833288 | 0.17967385 |
model_RF.model_performance(test) ModelMetricsRegression: drf ** Reported on test info. ** MSE: 16405336914.530426 RMSE: 128083.3202041953 MAE: 71572.37981480274 RMSLE: 0.17712324625977907 Mean Residual Deviance: 16405336914.530426As will probably be seen from above, DRF merely missed the purpose of RMSE underneath $123k for on every the cross-validation and on test dataset.
Now, let’s try and match a deep learning model, as soon as extra tuning the parameters with Grid Search.
g= h2o.grid.H2OGridSearch( H2ODeepLearningEstimator( nfolds=nfolds, fold_assignment="Modulo", keep_cross_validation_predictions=True, reproducible=True, seed=123), hyper_params={ "epochs": [20, 25], "hidden": [[20, 20, 20], [25, 25, 25]], "stopping_rounds": [0, 5], "stopping_tolerance": [0.006] }, search_criteria={ "method":"RandomDiscrete", "max_models":10, "stopping_metric": "rmse", "max_runtime_secs":60 } ) g.apply(x, y, apply) g #deeplearning Grid Build progress: |███████████████████████████████████████| 100% # epochs hidden stopping_rounds stopping_tolerance #0 16.79120554889533 [25, 25, 25] 0 0.006 #1 3.1976799968879086 [25, 25, 25] 0 0.006 # model_ids #0 Grid_DeepLearning_train_model_python_1628864392402_55_model_0 #1 Grid_DeepLearning_train_model_python_1628864392402_55_model_1 # residual_deviance #0 1.6484562934855278E10 #1 2.1652538389322113E10 Model 4
model_DL = H2ODeepLearningEstimator(epochs=30, model_id='dl_house', nfolds=nfolds, stopping_rounds=7, stopping_tolerance=0.006, hidden=[30, 30, 30], reproducible=True, fold_assignment="Modulo", keep_cross_validation_predictions=True, seed=123 ) %time model_DL.apply(x, y, apply) #deeplearning Model Build progress: |██████████████████████████████████████| 100% #Wall time: 55.7 s model_DL.cross_validation_metrics_summary().as_data_frame()| indicate | sd | cv_1_valid | cv_2_valid | cv_3_valid | cv_4_valid | cv_5_valid | ||
|---|---|---|---|---|---|---|---|---|
| 0 | mae | 72458.19 | 1241.8936 | 71992.18 | 73569.984 | 75272.75 | 70553.38 | 70902.65 |
| 1 | mean_residual_deviance | 1.48438886E10 | 5.5005555E8 | 1.42477005E10 | 1.59033723E10 | 1.54513889E10 | 1.48586271E10 | 1.37583514E10 |
| 2 | mse | 1.48438886E10 | 5.5005555E8 | 1.42477005E10 | 1.59033723E10 | 1.54513889E10 | 1.48586271E10 | 1.37583514E10 |
| 3 | r2 | 0.8899759 | 0.0023493338 | 0.89545286 | 0.8901592 | 0.885028 | 0.89008224 | 0.88915724 |
| 4 | residual_deviance | 1.48438886E10 | 5.5005555E8 | 1.42477005E10 | 1.59033723E10 | 1.54513889E10 | 1.48586271E10 | 1.37583514E10 |
| 5 | rmse | 121793.58 | 2259.6975 | 119363.734 | 126108.58 | 124303.62 | 121895.97 | 117296.0 |
| 6 | rmsle | 0.18431115 | 0.0011469581 | 0.18251595 | 0.18650953 | 0.18453318 | 0.18555655 | 0.18244053 |
As will probably be seen from the above desk (row 5, column 1), the indicate RMSE for cross-validation is 121793.58, which is underneath $123k.
model_DL.model_performance(test) #ModelMetricsRegression: deeplearning #** Reported on test info. ** #MSE: 14781990070.095192 #RMSE: 121581.20771770278 #MAE: 72522.60487846025 #RMSLE: 0.1834924698171073 #Mean Residual Deviance: 14781990070.095192As will probably be seen from above, the deep learning model could receive the purpose of RMSE underneath $123k on test dataset.
3. Finally, let’s apply a stacked ensemble of the fashions created in earlier steps. We might must repeat steps two and three until the easiest model (which is usually the ensemble model, nevertheless would not must be) has the minimal required effectivity on the cross-validation dataset. Note: only one model has to understand the minimal required effectivity. If a variety of fashions receive it, so we now have to pick the easiest performing one.
fashions = [model_GBM.model_id, model_RF.model_id, model_DL.model_id] #model_GLM.model_id, model_SE = H2OStackedEnsembleEstimator(model_id = 'se_gbm_dl_house', base_models=fashions) %time model_SE.apply(x, y, apply) #stackedensemble Model Build progress: |███████████████████████████████████| 100% #Wall time: 2.67 s #model_SE.model_performance(test) #ModelMetricsRegressionGLM: stackedensemble #** Reported on test info. ** #MSE: 130916347835.45828 #RMSE: 361823.6418967924 #MAE: 236448.3672215734 #RMSLE: 0.5514878971097109 #R^2: 0.015148783736682492 #Mean Residual Deviance: 130916347835.45828 #Null ranges of freedom: 2150 #Residual ranges of freedom: 2147 #Null deviance: 285935013037402.7 #Residual deviance: 281601064194070.75 #AIC: 61175.193832813566As will probably be seen from above, the stacked ensemble model could not attain the required effectivity, neither on the cross-validation, nor on the test dataset.
4. Now let’s get the effectivity on the test info of the chosen model/ensemble, and be sure that this moreover reaches the minimal purpose on the test info.
Best Model
The model that performs best in phrases of indicate cross-validation RMSE and RMSE on the test dataset (every of them are underneath the minimal purpose $123k) is the gradient boositng model (GBM), which is the Model 2 above.
model_GBM.model_performance(test) #ModelMetricsRegression: gbm #** Reported on test info. ** #MSE: 14243079402.729088 #RMSE: 119344.37315068142 #MAE: 65050.344749203745 #RMSLE: 0.16421689257411975 #Mean Residual Deviance: 14243079402.729088 # save the fashions h2o.save_model(model_GBM, 'best_model (GBM)') # the final word best model h2o.save_model(model_SE, 'SE_model') h2o.save_model(model_GBM, 'GBM_model') h2o.save_model(model_RF, 'RF_model') h2o.save_model(model_GLM, 'GLM_model') h2o.save_model(model_DL, 'DL_model')