How to Do a T-test in Python?

T-test: The hottest speculation check

In as we speak’s data-driven world, knowledge is generated and consumed on a each day foundation. All this knowledge holds numerous hidden concepts and knowledge that may be exhausting to uncover. Data scientists generally method this downside utilizing statistics to make educated guesses about knowledge.

Any testable assumption concerning knowledge is referred to as a speculation. Hypothesis testing is a statistical testing technique used to experimentally confirm a speculation. In knowledge science, speculation testing examines assumptions on pattern knowledge to draw insights about a bigger knowledge inhabitants.

Hypothesis testing varies based mostly on the statistical inhabitants parameter getting used for testing. One of the most typical issues in statistics is evaluating the means between two populations. The commonest method to that is the t-test. In this text, we are going to talk about about this fashionable statistical check and present some easy examples in the Python programming language.

What is a T-Test?

The t-test was developed by William Sealy Gosset in 1908 as Student’s t-test. Sealy printed his work beneath the pseudonym “Student”. The goal of this check is to evaluate the technique of two associated or unrelated pattern teams. It is used in speculation testing to check the applicability of an assumption to a inhabitants of curiosity. T-tests are solely relevant to two knowledge teams. If you need to evaluate greater than two teams, then you have got to resort to different assessments equivalent to ANOVA.

When are T-Tests used?

A one-tailed t-test is a directional check that determines the connection between inhabitants means in a single route, i.e., proper or left tail. A two-tailed t-test is a non-directional check that determines if there’s any relationship between inhabitants means in both route.

So if you count on a single worth speculation, like mean1=mean2, a one-tailed check could be preferable. A two-tailed check makes extra sense in case your speculation assumes means to be larger than or lower than one another.

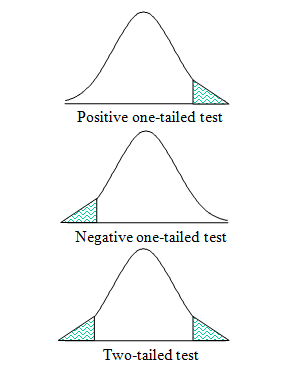
What are the assumptions?

T-tests are parametric assessments for figuring out correlations between two samples of knowledge. T-tests require knowledge to be distributed in accordance to the next assumptions about unknown inhabitants parameters:

• Data values are impartial and steady, i.e., the measurement scale for knowledge ought to observe a steady sample.
• Data is usually distributed, i.e., when plotted, its graph resembles a bell-shaped curve.
• Data is randomly sampled.
• Variance of knowledge in each pattern teams is analogous, i.e., samples have virtually equal commonplace deviation (relevant for a two-sample t-test).

What are the steps concerned in T-Tests?

Like any speculation check, t-tests are carried out in the next order of steps:

• State a speculation. A speculation is assessed as a null speculation ( H0) and an alternate speculation (Ha) that rejects the null speculation. The null and alternate hypotheses are outlined in accordance to the kind of check being carried out.
• Collect pattern knowledge.
• Conduct the check.
• Reject or fail to reject your null speculation H0.

What are the parameters concerned in T-tests?

In addition to group means and commonplace deviations, there are different parameters in t-tests which are concerned in figuring out the validity of the null speculation. Following is a checklist of these parameters that may repeatedly be talked about forward when implementing t-tests:

• T-statistic: A t-test reduces your complete knowledge into a single worth, referred to as the t-statistic. This single worth serves as a measure of proof towards the acknowledged speculation. A t-statistic shut to zero represents the bottom proof towards the speculation. A bigger t-statistic worth represents sturdy proof towards the speculation.
• P-value: A p-value is the proportion chance of the t-statistic to have occurred by likelihood. It is represented as a decimal, e.g., a p-value of 0.05 represents a 5% chance of seeing a t-statistic no less than as excessive because the one calculated, assuming the null speculation was true.
• Significance stage: A significance stage is the proportion chance of rejecting a true null speculation. This can also be referred to as alpha.

What are the various kinds of T-Tests?

There are three predominant varieties of t-tests relying on the quantity and kind of pattern teams concerned. Let us get into the small print and implementation of every sort:

1. One-Sample T-Test

An one-sample t-test compares the imply of a pattern group to a hypothetical imply worth. This check is carried out on a single pattern group, therefore the identify; one-sample check. The check goals to determine whether or not the pattern group belongs to the hypothetical inhabitants.

Formula

t=m-s/nWhere,t= T-statisticm= group imply= preset imply worth (theoretical or imply of the inhabitants)s= group commonplace deviationn= dimension of group

Implementation

Step 1: Define hypotheses for the check (null and different)

State the next hypotheses:

• Null Hypothesis (H0): Sample imply (m) is lower than or equal to the hypothetical imply. (<=m)
• Alternative Hypothesis (Ha): Sample imply (m) is bigger than the hypothetical imply. (>m)

Step 2: Import Python libraries

Start with importing required libraries. In Python, stats library is used for t-tests that embody the ttest_1samp perform to carry out a one-sample t-test.

import numpy as np from scipy import stats from numpy.random import seed from numpy.random import randn from numpy.random import regular from scipy.stats import ttest_1samp

Step 3: Create a random pattern group

Create a random pattern group of 20 values utilizing the traditional perform in the numpy.random library. Setting the imply to 150 and commonplace deviation to 10.

seed=(1) pattern =regular(150,10,20) print(‘Sample: ‘, pattern)

Step 4: Conduct the check

Use the ttest_1samp perform to conduct a one-sample t-test. Set the popmean parameter to 155 in accordance to the null speculation (pattern imply<=inhabitants imply). This perform returns a t-statistic worth and a p-value and performs a two-tailed check by default. To get a one-tailed check outcome, divide the p-value by 2 and evaluate towards a significance stage of 0.05 (additionally referred to as alpha).

t_stat, p_value = ttest_1samp(pattern, popmean=155) print(“T-statistic worth: “, t_stat) print(“P-Value: “, p_value)

A detrimental t-value signifies the route of the pattern imply excessive, and has no impact on the distinction between pattern and inhabitants means.

Step 5: Check standards for rejecting the null speculation

For the null speculation, assuming the pattern imply is lesser than or equal to the hypothetical imply:

• Reject the null speculation if p-value <= alpha
• Fail to reject the null speculation if p-value > alpha
• Reject or fail to reject speculation based mostly on outcome

The outcomes point out a p-value of 0.21, which is bigger than = 0.05, failing to reject the null speculation. So this check concludes that the pattern imply was lower than the hypothetical imply.

2. Two-Sample T-test

A two-sample t-test, often known as an independent-sample check, compares the technique of two impartial pattern teams. A two-sample t-test goals to evaluate the technique of samples belonging to two totally different populations.

Formula

t=mA- mBs2nA+s2nBWhere,mA and mB = technique of the 2 samplesnA and nB = sizes of the 2 sampless2 = widespread variance of the 2 samples

Implementation

Step 1: Define the hypotheses (null and different)

State the next hypotheses for significance stage =0.05:

• Null Hypothesis (H0): Independent pattern means (m1 and m2) are equal. (m1=m2)
• Alternative Hypothesis (Ha): Independent pattern means (m1 and m2) usually are not equal. (m1!=m2)

Step 2: Import libraries

Start with importing required libraries. Like beforehand, stats library is used for t-tests that embody the ttest_ind perform to carry out impartial pattern t-test (two-sample check).

from numpy.random import seed from numpy.random import randn from numpy.random import regular from scipy.stats import ttest_ind

Step 3: Create two impartial pattern teams

Using the regular perform of the random quantity generator to create two usually distributed impartial samples of fifty values, totally different means (30 and 33), and virtually the identical commonplace deviations (16 and 18).

# seed the random quantity generator seed(1) # create two impartial pattern teams sample1= regular(30, 16, 50) sample2=regular(33, 18, 50) print(‘Sample 1: ‘,sample1) print(‘Sample 2: ‘,sample2)

Step 4: Conduct the check

Use the ttest_ind perform to conduct a two-sample t-test. This perform returns a t-statistic worth and a p-value.

t_stat, p_value = ttest_ind(sample1, sample2) print(“T-statistic worth: “, t_stat) print(“P-Value: “, p_value)

Step 5: Check standards for rejecting the null speculation

For the null speculation, assuming pattern means are equal:

• Reject the null speculation if p-value <= alpha
• Fail to reject the null speculation if p-value > alpha
• Reject or fail to reject every speculation based mostly on the outcome

The outcomes point out a p-value of 0.04, which is lower than alpha=0.05, rejecting the null speculation. So this two-sample t-test concludes that the imply of the primary pattern is both larger or lower than the imply of the second pattern.

3. Paired T-Test

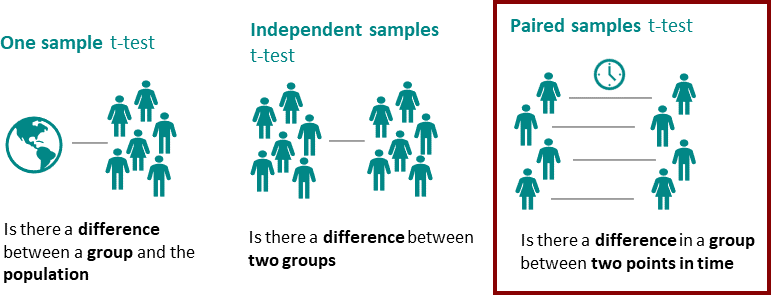
A paired t-test, often known as a dependent pattern check, compares the technique of two associated samples. The samples belong to the identical inhabitants and are analyzed beneath different circumstances, e.g., at totally different factors in time. This check is generally fashionable for pretest/posttest sort of experiments the place a pattern is studied earlier than and after its circumstances are different with an experiment.

Formula

t=ms/nWhere,t= T-statisticm= group means= group commonplace deviationn= dimension of group

Implementation

Step 1: Define hypotheses (null and different)

State the next hypotheses for significance stage =0.05:

• Null Hypothesis (H0): Dependent pattern means (m1 and m2) are equal (m1=m2).
• Alternative Hypothesis (Ha): Dependent pattern means (m1 and m2) usually are not equal (m1!=m2)

Step 2: Import Python libraries

Start with importing required libraries. Import the ttest_rel perform from the stats library to carry out a dependent pattern t-test (paired t-test).

from numpy.random import seed from numpy.random import randn from numpy.random import regular from scipy.stats import ttest_rel

Step 3: Create two dependent pattern teams

For simplicity, use the identical random samples from the two-sample implementation. We can assume the samples are from the identical inhabitants.

# seed the random quantity generator seed(1) # create two dependent pattern teams sample1= regular(30, 16, 50) sample2=regular(33, 18, 50) print(‘Sample 1: ‘,sample1) print(‘Sample 2: ‘,sample2)

Step 4: Conduct the check

Use ttest_rel perform to conduct a two-sample t-test on two dependent/associated samples. This perform returns a t-statistic worth and a p-value.

t_stat, p_value = ttest_rel(sample1, sample2) print(“T-statistic worth: “, t_stat) print(“P-Value: “, p_value)

Step 5: Check standards for rejecting the null speculation

For the null speculation assuming pattern means are equal:

• Reject the null speculation if p-value <= alpha
• Fail to reject the null speculation if p-value > alpha
• Reject or fail to reject speculation based mostly on outcome

The outcomes point out a p-value of 0.05, which is equal to 0.05, therefore rejecting the null speculation. So this paired t-test concludes that the imply of the primary pattern is both larger or lower than the imply of the second pattern.

Why are t-tests helpful in knowledge evaluation?

The t-test is a versatile device. Data scientists use these assessments to confirm their knowledge observations and the chance of these observations being true. It is a tried-and-tested method to evaluating observations with out the overhead of involving your complete inhabitants knowledge in the evaluation.

From testing the acquisition numbers of a new product to evaluating financial development amongst nations, speculation assessments are an essential statistical device for companies and one of the essential instruments in a statistician’s arsenal. Wherever knowledge is concerned, t-tests will play an important position in validating knowledge findings.

If you have an interest in pursuing a profession in knowledge science, ensure to try Beyond Machine!

The put up How to Do a T-test in Python? appeared first on Datafloq.